Who We Are
The U.S. Army Combat Capabilities Development Command, known as DEVCOM, Army Research Laboratory is the Army’s research laboratory strategically placed under the Army Futures Command. ARL is the Army’s sole foundational research laboratory focused on cutting-edge scientific discovery, technological innovation, and transitioning capabilities for the future Army.

Dr. Patrick
Baker

COL Robert
Murray

Mr. Joseph
Alexander

Ms. Cynthia
Bedell

Dr. Barton
Halpern

Ms. Kimberly
Ploskonka

Dr. Scott
Schoenfeld

Ms. Teresa
Kines
The DEVCOM Army Research Laboratory is organized by a three-directorate structure that is designed to strengthen synchronization, coordination, and integration of the full ARL team and ensure that ARL supports Army priorities and achieves mission success of operationalizing science at the speed of relevance.
DEVCOM ARL seeks to remain at the forefront of executing the highest-quality research possible, building leaders in the scientific community, setting a bold Army-relevant science agenda and pushing beyond existing boundaries in search of new ideas.
ARL fully integrates our internal and external foundational research efforts to shape future concepts with scientific research and knowledge, and deliver technology for modernization solutions to win in the future operating environment.
Army Research Office
ARL’s Army Research Office Directorate (ARO), founded in 1951 as the Army Research Office and based in Research Triangle Park, N.C., has more than 100 scientists, engineers and support staff, who manage the Army’s extramural research program. ARO drives cutting-edge and disruptive scientific discoveries that will enable crucial future Army technologies and capabilities through high-risk, high pay-off research opportunities.
Research Business Directorate
ARL’s Research Business Directorate (RBD) centralizes the laboratory’s business operations such as laboratory operations, strategic partnerships and plans, programs and budget synchronization, and focuses on facilitating strategic decision-making among cross-disciplinary internal and external teams.
Army Research Directorate
ARL’s Army Research Directorate (ARD) focuses on exploiting concept development, discovery, technology development, and transition of the most promising disruptive science and technology to deliver to the Army fundamentally advantageous science-based capabilities through laboratory’s research competencies. This intramural research directorate also manages the laboratory’s essential research programs, which are flagship research efforts focused on delivering defined outcomes.
DEVCOM ARL’s unique facilities and diverse, preeminent workforce comprise the largest source of world-class integrated research in the Army.
The laboratory’s facilities and regional locations focus on technology areas critical to performing disruptive foundational research to answer the hardest S&T questions for Army modernization and future Army capabilities.
DEVCOM ARL operates laboratories and experimental facilities, offices and many one-of-a-kind facilities in several prominent locations around the United States. In many cases, the laboratory’s collaborations with other nations, laboratories, academia, and industry span the globe.
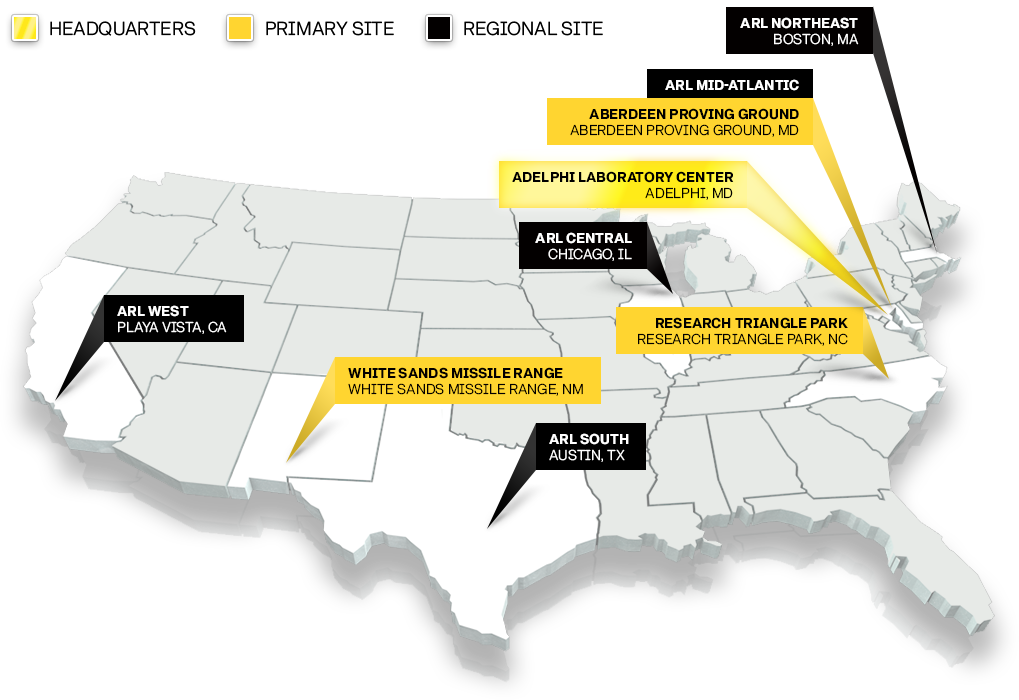
Learn more about each of our locations, including contacts and visitor information:
The diversity of our laboratories coupled with a world-class research team are leading to fundamentally advantageous change to the Army – that is rooted in the creation and exploitation of scientific knowledge – at the speed of relevance.
This book provides an overview of DEVCOM ARL’s facilities at our locations and how they help ARL accomplish its mission of operationalizing science for transformational overmatch. As you learn about our facilities, you will quickly see why DEVCOM ARL is leading the Department of Defense in the areas of discovery, innovation, and transition of basic and applied research.










